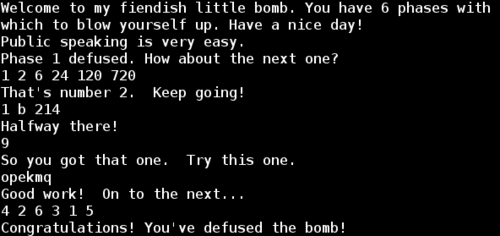
Defusing the binary bomb

I recently discovered a popular reverse engineering assignment in many university CS programs called the Binary Bomb. I didn’t have it at my school, but it looked like a fun project so I decided to try it.

The binary bomb is a simple command line program that asks you to enter a particular secret string. If type the incorrect string, the program explodes by printing out BOOM!!! and terminating. If you enter the correct string, the program proceeds to the next phase, which expects another particular string. In a typical classroom setup, each explosion will automatically notify your professor and deduct a small percentage from your final assignment grade.

The goal is to use a debugger to reverse engineer the executable in order to find the expected string for each phase and prevent the bomb from blowing up.

I completed the project over a few days, and have written a detailed walkthrough below.

If you’d like to play along at home, the original executable is up on the Internet Archive. Make sure you are running the executable on a 64-bit Linux box or VM.

Table of Contents

Phase 1
Phase 2
Phase 3
Phase 4
Phase 5
Phase 6
Secret Phase

Phase 1

I fired up gdb, added some breakpoints before and after the first input string required for the bomb. Then I stepped through the disassembled instructions to find a function called phase_1.

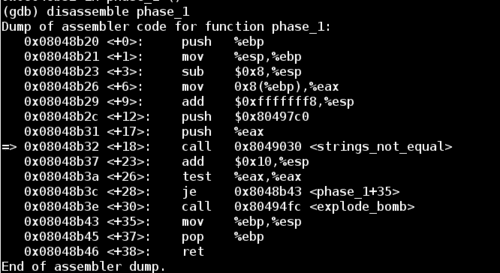
Note that between the beginning and end of phase_1 there is a call to the function strings_not_equal.

So we have two options here to beat phase 1:

1. Change the je (jump if equal instruction) to be a jne (jump if not equal), which will skip over explode_bomb to take us to the next phase. This method is easy to do, but it doesn’t actually give us the pass code for the first phase. So we would have to do this jump every time.

2. Dive into the strings_not_equal call and explore the code. There will likely be a string comparison in there that will reveal the string for this phase. In this way we can simply type in the string to beat phase 1 and go into phase 2 in the expected way.

Let’s disassemble strings_not_equal:

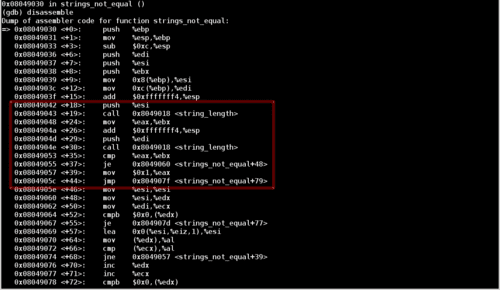
Notice that there are two calls to a function called string_length, followed by a jump depending on the the result of these function calls. Furthermore, notice that the registers esi and edi are pushed onto the stack before their respective string_length calls. This tells us that these registers are used as function arguments.

These instructions tell us that the function first compares the length of the input string before even checking if the user’s input matches the password.

Let’s examine the argument passed to the first string_length call:

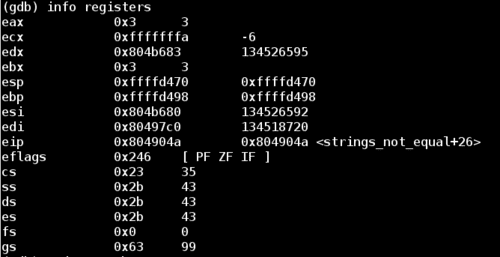
Note that we are looking for the value of the register esi, which is stored at 0x804b680. Let’s examine it as a string:

In this case, esi points to 123 which is what I typed in for my attempt for this phase.

Now let’s take a look at edi which is the register used in the second string_length call, we will see what the program is comparing our input string against, which should be the password to phase 1.

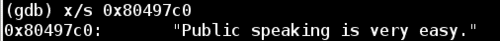
Let’s run the binary bomb and try it out:

Phaes 1 complete!

Phase 2

We can start by disassembling the phase_2 function just like we did for phase_1:

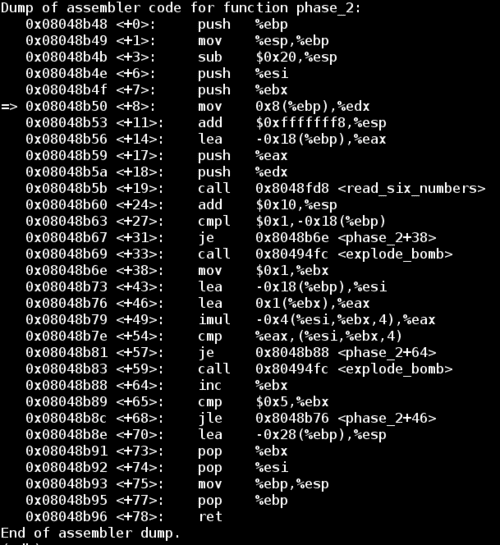
While the read_six_numbers function hints that this round will be looking for 6 numbers of input, it doesn’t really tell us anything about the values of these numbers. Notice the two explode_bomb calls in phase_2. Let’s add some breakpoints throughout the function and enter 012345 as our input.

The first explode_bomb call is after a comparison between the constant 0x1 and the value at address (%ebp - 0x18). Examining the memory location reveals that the value is 0. After some trial and error I discovered that this is the first number of my attempted password 012345. We can prove this by examining the values in memory of offsets other than 0x18.

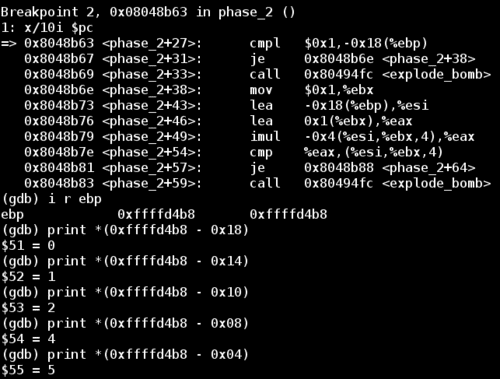
Now we know (%ebp - 0x18) corresponds to the first element of our input. If we want to avoid the first explode_bomb call, then the first cmpl (comparison instruction) must consider the values at the two addresses to be equal. This means the first digit of this password must be 1.

Now if we restart the bomb and use this new knowledge, we can bypass the first comparison and make it to the second one.

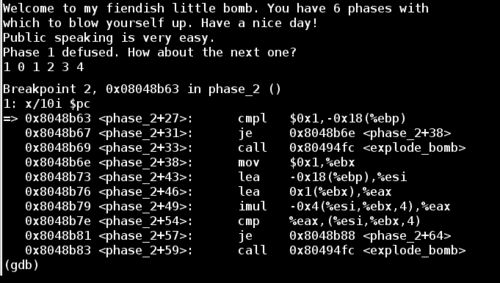
The second comparison is slightly more complicated and depends on the result of a (signed) multiplication. First we multiply (%esi - 0x4 + 4*%ebx) by %eax, and then store the result in %eax. In our case it gives us the following:

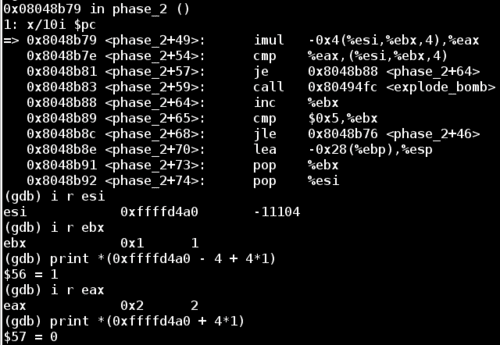
Now we meet the second comparison statement. The right hand side is simply an index to the current element of our input. This iteration it’s comparing the value in %eax to the second input value. If this comparison is not-equal, then the bomb will explode. Since the value of eax is 2, this means that the second digit of our input should be 2.

This time instead of re-running the program, we can just set the value directly in memory.

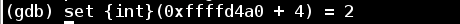
Now we reach the third round of the phase_2 loop. Let’s take a look at %eax again to see the expected digit.

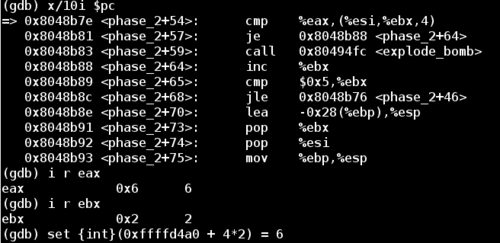
Doing this one more iteration reveals that the program expects the first 4 digits of the 6 digit password to have values 1 2 6 24. These are not arbitrary numbers. The pattern looks like increasing factorial digits. Notice that 1 2 6 24 is 1! 2! 3! 4!

Based on the function name, we can make the guess that the required password is just 6 numbers, and each one is the factorial of its 1-based index. This would be 1! 2! 3! 4! 5! 6! or 1 2 6 24 120 720

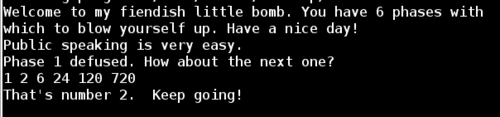
Success!

Phase 3

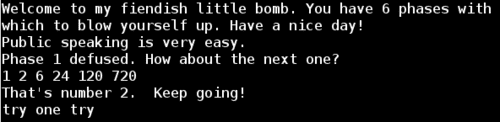
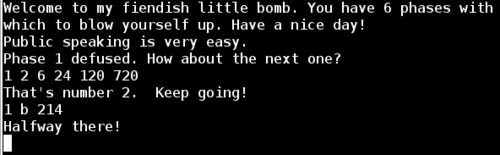
I restarted the program in gdb, set a breakpoint at the phase_3 function, and entered the passwords we’ve found so far for phase 1 and 2. Then I entered an initial guess for phase 3 of try one try.

Looking at the first dozen lines of the disassembled phase_3 function, note the call to sscanf. If we examine the arguments passed to this function, then we can figure out the input format of the password.

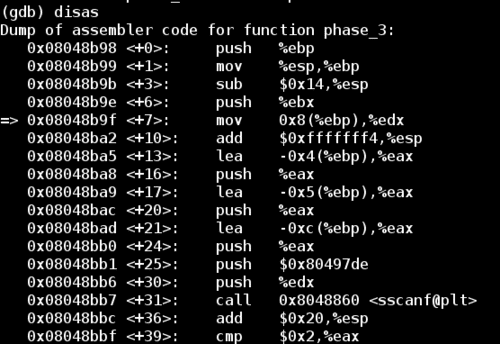
Notice that our input string and a format string was passed into sscanf. The format string is in the format %d %c %d, so it expects an integer, a character, and another integer.

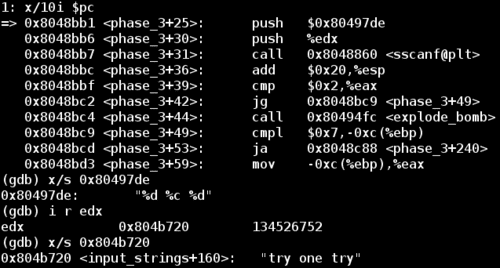
Since I entered `ry one tryas my initial guess, this does not fit the format that this call tosscanfexpects. This will causesscanfto return and set%eax to 0

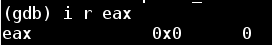
This would result in the comparison of %eax and 0x2 NOT taking the corresponding jump, and cause the bomb to explode.

So now I restarted the application with a better guess. Now that jump after the %eax comparison will succeed, we run into another conditional check. Examining the value in memory at (%ebp - 0xc) shows that the program is comparing the first number of our input to the value 7, and jumping (to avoid an explosion) if the number is less than or equal to 7. Since our input number was 1, this condition is true and we skip this call to explode_bomb. So far so good.

The next line of interest is a jmp statement which will jump to the offset of the value stored at (0x80497e8 + %eax*4).

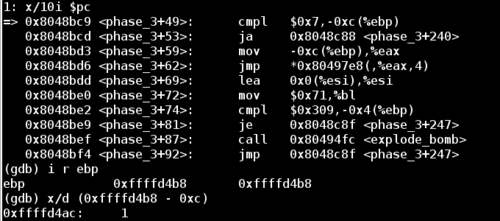
At this point %eax is set to the first number in our input string, so our jump takes us to the following position:

The next comparison examines our third input value (an integer) stored at (%ebp - 0x4) and checks it against the value 0xd6, or 214 in decimal.

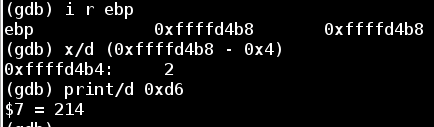
In order to beat this comparison, we can restart the app again with the following input:

Then, the final comparison checks our second input value (of type char) against %bl. Examining the value of %bl reveals that the application is expecting a b character for this situation

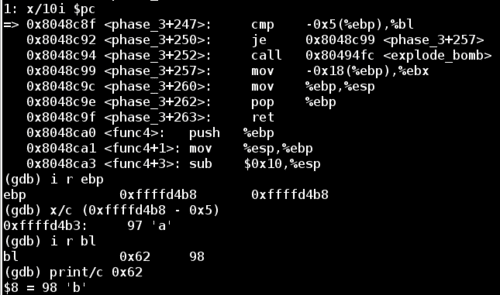
So we run the application one final time including everything we’ve learned about the phase_3 function, and we have now successfully completed phase 3!

Phase 4

Lets disassemble the phase_4 function next. Once again there is a call to sscanf, so let’s peek at the format string to see what kind of input this phase expects.

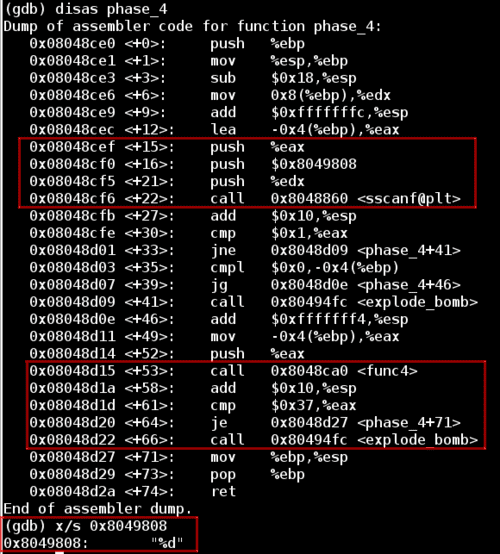
Notice that in the second highlighted segment our input value is passed into the function func4, and the result of this function is compared against 0x37 (55 in decimal).

Now let’s look at func4 in chunks in order to simplify it. First looking at section A, if the input value (located at [%ebp + 0x8] and then copied into %ebx) is less than or equal to 1, then the function jumps down to section B and sets %eax to 1, which will become the return value.

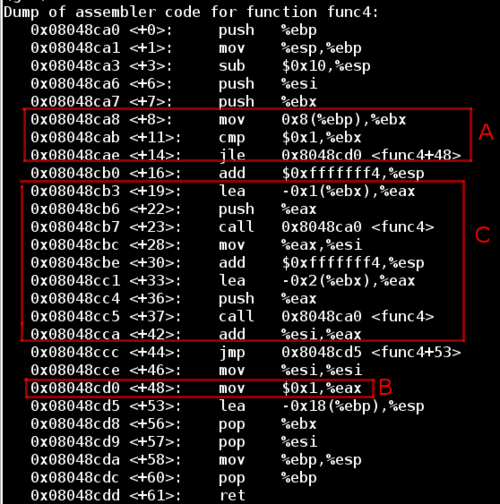
Otherwise, the function steps into section C which will call func4 recursively, passing in the original input decremented by one. This is followed by another call to func4, passing in the original input decremented by two. Then the result of these two function calls is summed and copied into %eax to become the return value of the function.

After stepping through a few iterations, I realized that the function was defined as func4(x) = func4(x-1) + func4(x-2), which looks like the Fibonnaci sequence of the input number.

However, notice that func4 will return 1 if the input is 0, whereas Fib(0) = 0. Therefore if we have an input of x = 2, func4 would return 1 for both the x - 1 = 1 and x - 2 = 0 calls.

Remember that the phase_4 function succeeds if the output of func4 was 0x37 (55 in decimal). Since the Fib(10) = 55 and we know that func4(0) = func(1) = 1, func4(2) = 2, then we just need to find an input x such that Fib(x + 1) = 55. Since Fib(10) = Fib(9 + 1) = 55, we know that the solution for this phase is 9.

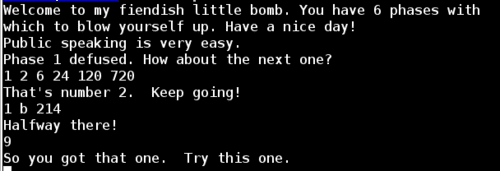
Phase 5

Let’s look at the first chunk of the disassembled phase_5 function:

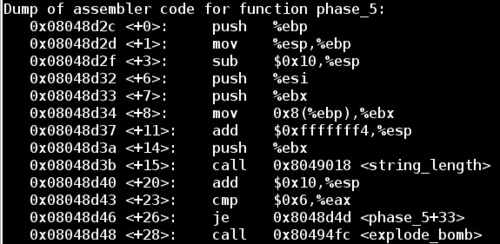
Notice the call to the string_length function, and the resulting jump away from explode_bomb if the return value is 6. Now we know that our input string must contain exactly 6 characters.

Looking down to the location of the jump, we have the following block of code that forms a loop. In this test run I’ve entered 123456 as my input.

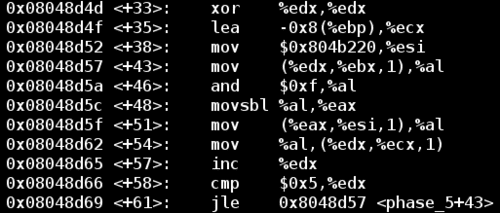
Notice that my input string is stored at %ebx.

In the loop above, the code takes our input value %ebx plus some offset %edx and copies it into %al. Then it performs a binary AND operation between 0xf and %al, and stores the result in %al and subsequently into %eax. Finally, it copies the character at [%esi + %eax] into %al, and into an initially empty string stored at [%ecx + %edx].

To start, let’s look at what is being stored at %esi:

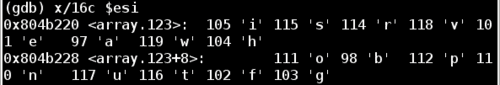
So there seems to be an array of characters stored at %esi. Each character from our input string is binary ANDed with 0xf. Then this resulting value is used as a lookup index in %esi to find the final character mapping.

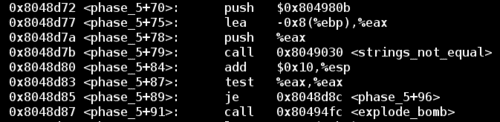
Now that we understand how the function works, we can examine the jump that avoids the final explode_bomb call. This code checks to see if the result of the logic above is equal to the string stored at 0x804980b

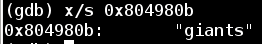
Now we know that the transformed version of our input string must equal giants. All we need to do is reverse engineer an input string that ends up as giants in the algorithm.

Taking another look at the substitution array stored at %esi:

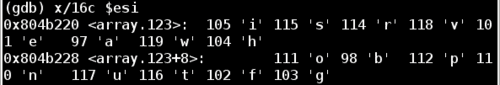
Notice that ‘g’ has an index of 15. Therefore we must find a character that when ANDed with 0xf will result in 15 decimal which is also 0xf hex. This type of operation is called a bitwise mask. To succeed here, we need to find a character that has 1111 as the least significant 4 bits. The 4 most significant bits don’t matter here. For example, the hex ASCII value for the letter o is 6F, which has a binary value of 0110 1111, so it fits our requirement.

We can continue in a similar fashion and find characters which match for remaining “iants”. My solution was the string opekmq, but there are many solutions for this phase.

Phase 6

Disassembling phase_6:

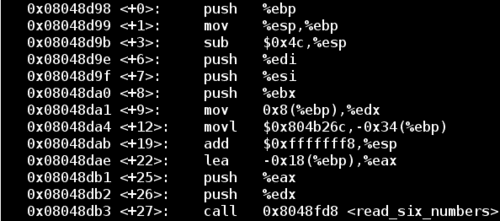
Notice the function call on the last line of the excerpt above reads six numbers from standard input, so now we know the first requirement of the password for this phase. I’ll enter the input 1 2 3 4 5 6 to satisfy the 6 digit requirement.

Next let’s look a little further down the function:

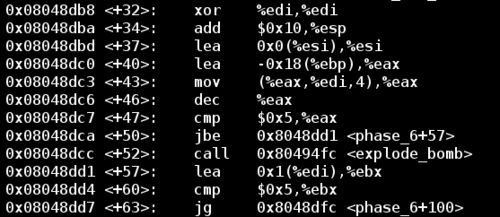
And after the jump:

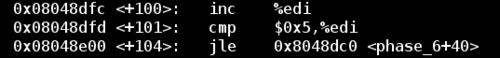
Notice that in the above block of code we have a loop. The counter for the loop is %edi, which is initially set to 0 using the XOR trick above, and the loop continues until %edi has reached a value of 6. Since %ebp - 0x18 is the location of the first input, this block of code is just iterating through all of the input values.

While iterating through all numbers, the function ensures that each number is less than 5. Notice that this comparison uses the jbe command, which does not test for the sign of the number. Keeping this in mind, this process can be summarized as the second requirement: Each of the six numbers must be between 1 and 6 inclusive.

Next, let’s examine the nested loop below:

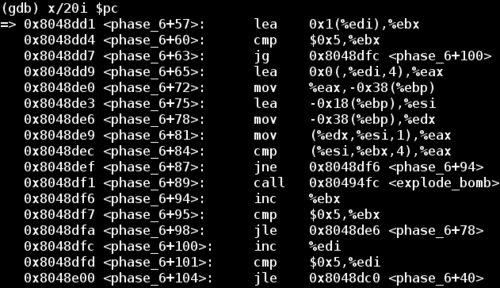
The loop has iterators %ebx and %edi. We’re comparing each number against every other number, and only jumping over the explode_bomb call if the numbers are not equal. Essentially this code is ensuring that the password consists of unique numbers 1-6.

The next restriction is the most complicated. Let’s go down near the final explode_bomb call:

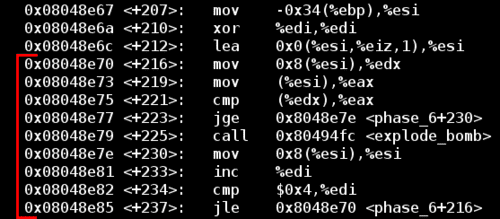
This part seems complicated initially. Ignore the early lea instruction since it’s a NOP to ensure code alignment. Skipping over that, I’ve highlighted the relevant loop above in red. After an initial %esi is set, the code is comparing the value at %esi, with the value at %esi + 0x8, and the bomb explodes if the value at %esi + 0x8 is less than the value at %esi.

But what are %esi and %esi + 0x8?

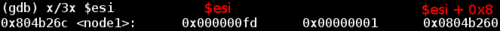
%esi points to a node data structure. Since debugging information is not included in this executable, we can’t find the definition of a node. But looking at what is given above we can gain some intuition about it. Let’s start by looking at what %esi + 0x8 leads to:

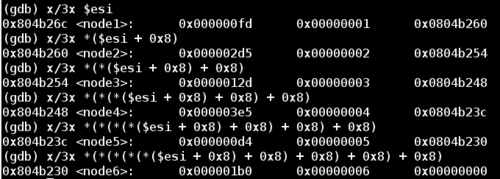
Notice that each of these nodes contain at least three things:

1. Firstly some numerical value
2. The input value corresponding to the node number (from the original 1 2 3 4 5 6 input)
3. A pointer to the next node.

This phase uses the common linked list data structure.

Some trial and error of input reveals two things. The first and second values in the above screenshot are identical for any order of input. So node1 will always have a first value of 0xfd and a second value of 0x1, node2 of 0x2d5 and 0x2, and so on. The only thing that changes is the pointer to the next node, which depends on the order of input values. For example, an input of 6 5 4 3 2 1 will result in node6 -> node5 -> node4 -> node3 -> node2 -> node1.

So now to beat this phase let’s take a closer look at conditions surrounding the explode_bomb call.

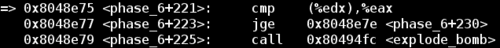
At this point %edx contains the pointer to the next node, and %eax contains the value of the current node’s first column number. Let’s call this first column number X. So this code compares if the current node’s X value is greater than the next node’s X value, and skips the explode_bomb call if this is the case.

So we have the following nodes and associated X values:

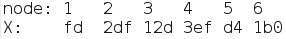
Since we are iterating over all nodes, and a node’s next pointer is related to the order of input, we just need to find the correct arrangement of numbers such that the current node’s X is always greater than its next node’s X value. More generally, we need to sort the numbers in decreasing order with respect to their X values.

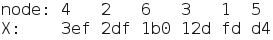
Now the nodes are sorted in order of decreasing X value. We can use the node indices as the password for this phase

Secret Phase

Although the bomb seems to be defused, poking around the disassembled main() reveals a function called secret_phase().

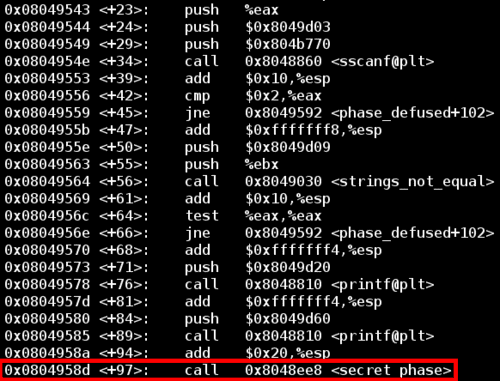
Like before, there are two ways to jump to this function call.

1. Alter a jmp instruction to go directly to the call to secret_phase(). This is simple but is risky since we don’t know if secret_phase() relies on any other logic in order to run successfully, that we would skip by jumping directly to it.
2. Take the time to figure out the true nature of the phase_defused function in order to enter the secret phase legitimately.

The analogy here is deciding whether to bash down a door and risk destroying anything behind it, or picking the lock and entering safely.

Once again, let’s go with the second option.

We’ll begin by looking at the sscanf call at the top of the code shown above. Let’s examine the format string and input:

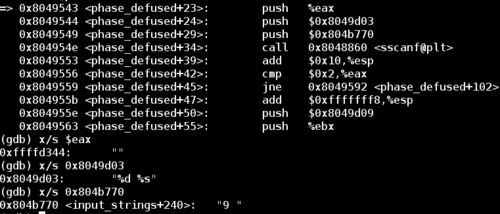
The first input to this sscanf call is the string 9, which we know is is the correct password for phase 4. The second part of the format string expects a string input. But what should this string be?

Let’s take a look at the inputs to the strings_not_equal call a little further down to get an idea of the string we need.

Now we know that to get into the secret phase, we need to add austinpowers to the end of the password for phase 4.

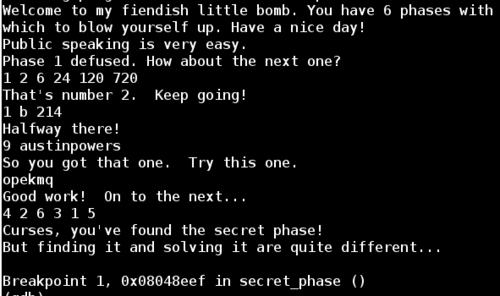
The secret phase takes a string input, converts it to an integer and checks that this integer is less than or equal to 0x3e9. If this is true, then it calls fun7 and expects the return value to be 7.

Since 0x3e9 is 1001 decimal, I entered 1001 as my first guess for the secret phase password. Amazingly, this was the correct answer to the secret phase. At this point it was getting late and I didn’t spend the time to understand how fun7 works.

Be that as it may, this bomb has now been defused, and the world is safe once more.

If you are interested in the details of how fun7 works, I found a great write up by someone with more patience than me.

Thanks for reading along!